Oceanverse
Strictly use Geogebra to solve all the questions
Module 0
-
Plot the points \((2,3)\) and \((6,9)\) and find the distance between them without using the formula for distance.
-
Plot two vectors \(u=⟨3,−2⟩\) and \(v=⟨−1,5⟩\).
-
Find the angle between them.
-
Construct a perpendicular bisector of a given segment whose end points are \((0,6)\) and \((6,0)\).
-
Plot line \(y=3x\).
-
Graph the equation \(y=2x+3\) over the interval \([−5,5]\) and find the points where the graph intersects the x-axis and y-axis.
-
Explore the behavior of the quadratic function \(f(x)=x^2−4x+3\). Determine its vertex, axis of symmetry, and roots.
-
Find the angle between the lines with equations \(y=2x+3\) and \(y=−3x+2\).
-
Determine the angle of depression from the top of a building to a point on the ground 50 meters away from the base of the building, given that the height of the building is 30 meters.
-
Construct a right angled triangle with legs of lengths 3 units and 4 units. Find the length of the hypotenuse.
-
Find the centriod of the above triangle.
-
Enter a set of parametric equations, such as \(x(t)=cos(t)\) and \(y(t)=sin(t)\) to plot a circle.
-
Create two planes: Plane 1: \(2x−3y+z=6\), Plane 2: \(x+4y−2z=8\). Plot the two planes in a 3D coordinate system.
-
Determine the angle between the two planes. Are the planes intersecting? Is there any unique point in common? What do you infer from this?
Module A
1.Ram and Lakshman were two brothers, Ram’s pocket money was twice as Lakshman. The good boys that Ram and Lakshman were, they did not spend their pocket money on anything. They instead saved the same in their piggy bank. Every week, they would check their savings so far. Assume the first week’s savings was \((R_1,L_1)\) and second week’s \((R_2,L_2)\) and so on. They try plotting their weekly savings on a graph sheet. How will the points look like?
Sol.
2.Atul’s house is centered at origin \((0,0)\) he walks straight (along the x-axis) for 2 units and then takes a left and walks 1 unit to reach Bala’s house, after that he takes a right turn and walks for one unit and then a left turn and walks for one unit and reaches Chetan’s house. He continues in a similar style, takes a right turn 1 unit and then left turn one unit and reaches Divya’s house. Are the houses of Bala, Chetan and Divya on a straight line? What is the equation of this line? Plot this on Geogebra
Sol.
3.Plot the lines \(y=x\), \(y=2x\), \(y=10x\).
Sol.
4.Observe that they all pass through the origin. Why?
Sol.
5.Plot \(y=2x+1\). Observe, Why doesn’t it pass through the origin?
Sol.
6.Plot \(y=ax+b\), with \(a\) and \(b\) as parameters which you should be able to vary. What do you observe?
Sol.
6(a). Let a line be \(y=5x+6\). For what values of \(\alpha\) and \(\beta\) will the line \(y= \alpha x + \beta\) be parallel to the given line? When will it intersect the given line in the 3rd quadrant?
Sol.
7.Consider the following simultaneous equation:
\(2x+3y=7\)
\(3x+4y=10\)
Do you see a 2x2 matrix here? What is the importance of seeing a matrix in this problem? Why study matrices in general?
Do you observe that this problem can be retold as:
\(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right)\)
\(\left(
\begin{matrix}
x\\
y\\
\end{matrix}
\right)\)
=\(\left(
\begin{matrix}
7\\
10\\
\end{matrix}
\right)\)
Sol.
8.Consider a simple function \(f(x) = 3x+2\). This function is invertible right? Can you tell us what is \(\alpha\) such that \(f(\alpha)=17\)? Is such an \(\alpha\) unique? How did you find such an \(\alpha?\). Is this always possible?
Sol.
9.Consider the function \(f(x)=x^2-10\), what is \(f(5)\)?
Sol.
10.Consider the function \(f(x)=x^2-10\), if \(f(\alpha)=54\), what is \(\alpha\)?
Sol.
11.Consider the function \(g(x)=x^3-x^2-10x+2\), if \(g(x)=-22\) what is \(x\)?
Sol.
12.Do you know what is \(\mathbb{R}, \mathbb{R}^2 and\ \mathbb{R}^3\) ?
Sol.
13.Consider the function \(\phi : \mathbb{R}^2\rightarrow \mathbb{R}^2\) defined by \(\phi (x,y)=(2x+3y,3x+4y)\). Find x and y such that \(\phi (x,y)=(5,6)\). Obseve that (5,6) as well as (x,y) lies in \(\mathbb{R}^2\).
Sol.
14.Is the function \(\phi\) invertible? In the question above on matrices, we see that it is of the form \(A\vec{x}=b\). Note that we can invert the matrix, using the method that was taught to us in our high school to find out the value for the variables \(x\) and \(y\). This is one of the many applications of matrices.
Sol.
14(a). Take a random looking 2*2 matrix. Is it invertible? How often is it invertible?
Sol.
15.We will now see matrices as functions. Instead of \(\phi\) we will write the matrix itself:
\(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2\).
Sol.
16.Consider the function \(\left( \begin{matrix} 1 & 2 \\2 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2\). This matrix takes a few elements to the origin. What are those elements? Plot this using Geogebra.
Sol.
Module B
17.\(A\) is assigned \(0\), \(B:1\), \(C:2\), and so on up to \(Z:25\)
Assume you denoted every letter with a number, as given in the table above.
You need to encrypt the word \(SUDARSHANA\) which stands for the numbers: \(18, 20, 3, 0, 17, 18, 7, 0, 13,0\).
You encrypt this using a matrix given by : \(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right)\).
So \(SUDARSHANA\) will end up becoming: \(96, 134, 6, 9, 88, 123, 14, 21, 26, 39\).
Given these numbers, how will you decrypt the message and get back \(SUDARSHANA\)?
. This is a well known cryptographic protocol called the Hill Cipher. You can read more online.
Sol.
18.We encounter equations very often in our lives. Consider for example, the following situation at Baker’s Cafe. The manager has a very important estimate to make. Mostly, visitors at his cafe happen to be families and they are often comprised of Children and/or Adults. He observes that there are 3 adults and 1 child at a table and their bill turns out to be Rs.1200/-. There is yet another table with 2 children and 1 adult and their bill comes out to be Rs.1000/-. Can the manager estimate the consumption of a Child/Adult? This is popularly called the Simultaneous Equations and we all remember from our school days, multiple ways in which these can be solved.
\(3A + 1C = 1200\)
\(1A + 2C = 1000\)
Sol.
19.While we were taught the so called two variables and two unknowns, what if there were more equations than unknowns?
\(3A + 1C = 1200\)
\(1A + 2C = 1000\)
\(1A + 1C = 900\)
Sol.
20.Note that the previous question can be modelled as a matrix:
\(3A + 1C = 1200\)
\(1A + 2C = 1000\)
\(1A + 1C = 900\)
Observe this is same as :
\(\left( \begin{matrix} 3 & 1 \\1 & 2 \\1 & 1 \\\end{matrix}\right)\) \(\left( \begin{matrix} A\\ C\\ \end{matrix} \right)\) = \(\left( \begin{matrix} 1200\\ 1000\\ 900\\ \end{matrix} \right)\)
Now try to solve the previous problem.
Sol.
21.One obvious way to solve this, is to guess the values :-). Can you get closer to the solution by guessing? Note that there is no solution to this question. You can just reduce the error. Do you see why?
Sol.
22.In the figure below:
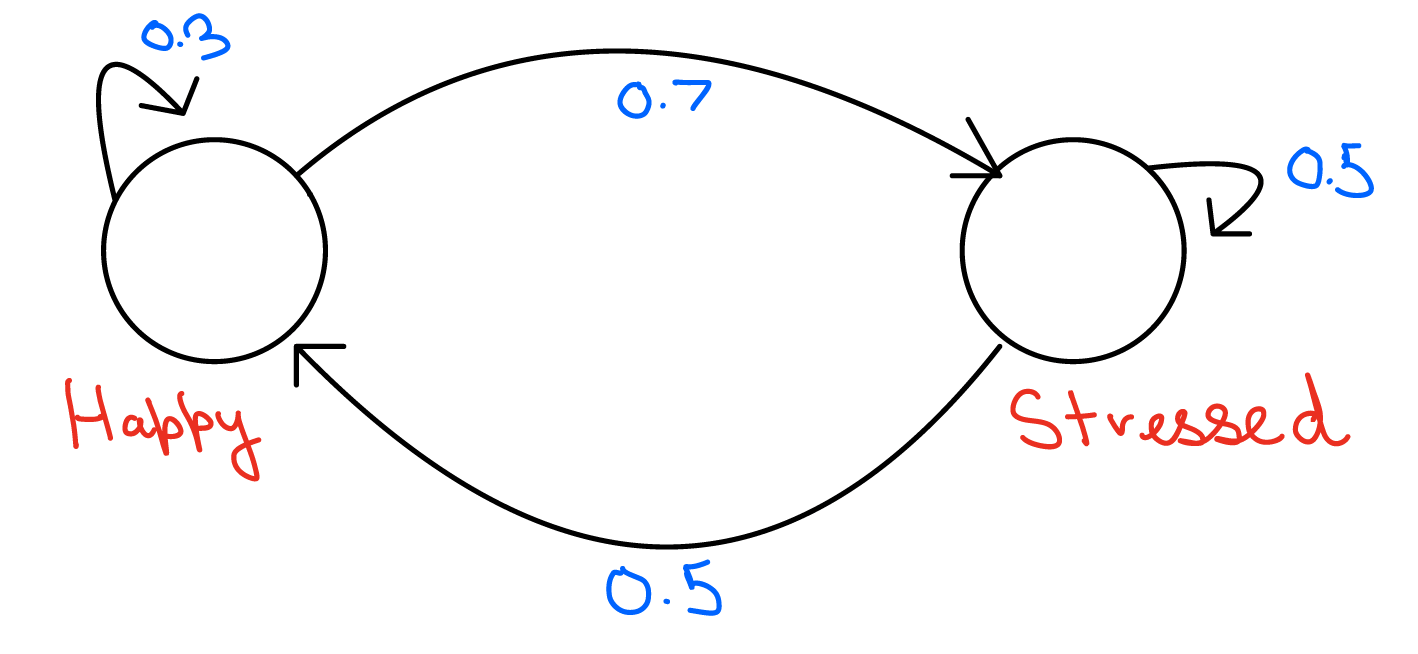 If 1000 people were to start in one state, what will be the distribution of people eventually? Write down a python script to find the convergence.
If 1000 people were to start in one state, what will be the distribution of people eventually? Write down a python script to find the convergence.
Sol.
23.In the figure below:
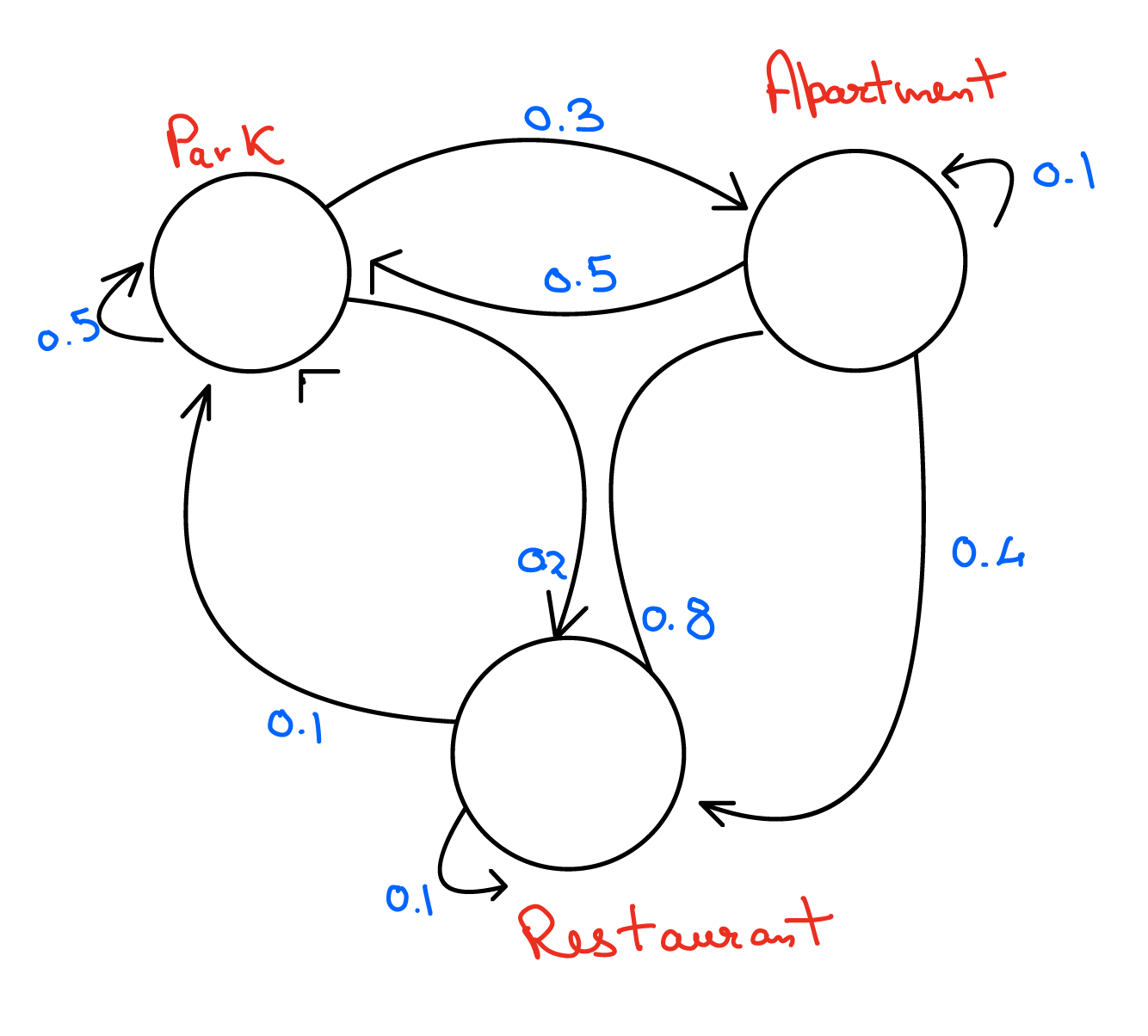 If 1000 people were to start in one state, what will be the distribution of people eventually? Write down a python script to find the convergence.
If 1000 people were to start in one state, what will be the distribution of people eventually? Write down a python script to find the convergence.
Sol.
Module C
24.Use Geogebra: Draw the vector \(\begin{bmatrix}1 \\ 1 \\ \end{bmatrix}\). Find out all those vectors which are perpendicular to this vector.
Sol.
25.Do you observe that we are asking for vectors \(\begin{bmatrix}x \\ y \\ \end{bmatrix}\) such that, \(\begin{bmatrix}1 & 1 \\ \end{bmatrix} \begin{bmatrix} x\\ y \\ \end{bmatrix}=0\)
Sol.
26.Use Geogebra and solve the above question with \(\begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}\) replaced by \(\begin{bmatrix}a \\ b \\ \end{bmatrix}\).Use \((a,b)\) as parameters and check what happens to \((x,y)\).
Sol.
27.What is \((x,y,z)\) satisfying the following equation? (Use Geogebra) \(\begin{bmatrix}1 & 2 & 3\\ \end{bmatrix} \begin{bmatrix} x\\ y \\ z\\ \end{bmatrix}=0\)
Sol.
28.Use Geogebra and plot all the points in the set below. \(T= \{ \alpha(1,2,1) | \alpha \in \mathbb{R}\}\)
Sol.
29.Use Geogebra and plot all the points in the set below. \(S= \{ \beta(2,7,3) | \beta \in \mathbb{R}\}\)
Sol.
30.Use Geogebra and plot all the points in the set below. \(W= \{\alpha(1,2,1) + \beta(2,7,3) | \alpha,\beta \in \mathbb{R}\}\)
Sol.
31.In the above set \(W\) find out all the points \((x,y,z)\) satisfying the following: (Use Geogebra) \(\begin{bmatrix}w_1 & w_2 & w_3\\ \end{bmatrix} \begin{bmatrix} x\\ y \\ z\\ \end{bmatrix}=0\) where \((w_1,w_2,w_3) \in W\). Note that \(w_i\)s are real numbers.
Sol.
32.Given the matrix \(A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}\), find out all the possible \((x,y,z)\) such that: \(\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix}=0\) Observe carefully, what has this question got to do with previous five questions in this module
Sol.
33.Given the matrix \(A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}\) what does the following three sets represent?
(i) \(\mathscr{R}=\{\alpha(1,2,3) + \beta(4,5,6) + \gamma(7,8,9) |\alpha, \beta, \gamma\in \mathbb{R}\}\)
(ii) \(C=\{\alpha(1,4,7) + \beta(2,5,8) + \gamma(3,6,9) | \alpha, \beta, \gamma \in \mathbb{R}\}\)
(iii) \(N=\{(x,y,z)|x(1,4,7) + y(2,5,8) + z(3,6,9) = 0 \}\)
Use only Geogebra :)
Sol.
34.Did you observe that every vector of \(\mathscr{R}\) is perpendicular to every vector of \(N\)?
Sol.
35.Consider the matrix \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}\). Draw the line \(2y+x=4\). Seeing the matrix \(B\) as a function \(B:\mathbb{R^2}\mapsto \mathbb{R^2}\),
where does \(B\) takes the line \(2y+x=4\)?
Where does it take:
i)\(2y+x=10\)
ii)\(2y+x=62\)
iii)\(2y+x=1800\)
Sol.
35(a).In general \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\), where does this function take \(2y+x=k\)?(where \(k\) is a constant)
Sol.
36.Consider a matrix \(A=\begin{bmatrix} 1 & 4 \\ 2 & 3\\ \end{bmatrix}\) and a vector $v$ = \(\begin{bmatrix} 1 \\ 1\\ \end{bmatrix}\) to what is it transformed?
36(a).Is it rotated?
36(b).Is the magnitude preserved?
36(c).What is the ratio of magnitude of \(Av\) to \(v\)?
Sol.
37.Given \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\). What is the range of this function?
Sol.
38.You have achieved the required wisdom if you have realized that:
\(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\).
“ \(B\) collapses a dimension “.
Sol.
Module D
39.Given the matrix \(M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}\). Use Geogebra to plot \(\mathscr{R}\), \(\mathscr{C}\) & \(\mathscr{N}\). what do you observe?
(i) \(\mathscr{R}=\{\alpha(1,3) + \beta(2,6) | \alpha, \beta\in \mathbb{R}\}\)
(ii) \(\mathscr{C}=\{\alpha(1,2) + \beta(3,6) | \alpha, \beta\in \mathbb{R}\}\)
(iii) \(\mathscr{N}=\{(x,y)| x(1,3) + y(2,6) = 0, \forall x,y\in \mathbb{R} \}\)
Sol.
40.Note that \(\mathscr{C}\) and \(\mathscr{N}\) are orthogonal.
Sol.
41.What is the null-space of \(M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}\) & the null-space of \(M^T\)?
Sol.
42.Do you observe that \(C(M)\) ⊥ \(N(M^T)\) , \(R(M)\) ⊥ \(N(M)\) ?
Sol.
43.Consider \(A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}\). What is \(N(A)\), \(C(A)\), \(R(A)\), \(N(A^T)\).
Sol.
44.Consider a 4x4 matrix \(M\): \(\mathbb{R^4}\mapsto \mathbb{R^4}\) whose range is
a) \(4-Dimension\)
b) \(3-Dimension\)
c) \(2-Dimension\)
d) \(1-Dimension\)
e) \(0-Dimension\)
Give an example each for all the above 5 cases.
Sol.
45.Consider \(A : \mathbb{R^{3}} \to \mathbb{R^{3}}\)
a) Show that if the range contains a point \((a,b,c)\), then it should contain the entire set \(S\), defined by:
\(S= \{\alpha(a, b,c)| \alpha \in \mathbb{R}\}\).
b) Show that if the range contains the points \((a,b,c)\) and \((d,e,f)\), then the range contains the entire set \(T\) defined by:
\(T=\{\alpha(a,b,c) + \beta(d,e,f) \thinspace|\thinspace \alpha,\beta\in \mathbb{R}\}\).
c) Note: \(S\) is of the dimension \(1\), but \(T\) need’nt be of dimension \(2\). Think!
Sol.
Module E
46.Give an example of two \(2-dim\) subspaces in \(\mathbb{R^{3}}\). Let us call it \(S_1, S_2\).
Sol.
47.Let \(S_3\) be all those vectors perpendicular to \(S_1\). \(S_4\) be that of \(S_2\).
Sol.
48.Find a matrix \(M\) whose Null-Space is \(S_3\). column space is \(S_2\).
Sol.
49.What does \(S_1\) and \(S_4\) represent?
Sol.
50.Do you observe there is a bijection from \(S_1 \to S_2\)?
Sol.
Module F
51.Imagine a situation of war in 1800’s.Country A wants to send a letter to Country B such that their enemy country can’t understand the message.How can you help the country A in this situation?
Sol.
In the scenario of wartime communication in the 1800s, Country A could employ the Caesar cipher to encode their messages to Country B. The Caesar cipher is a substitution cipher where each letter in the plaintext is shifted a certain number of places down or up the alphabet. By agreeing on a specific shift value beforehand, known as the "key," Country A could encode their messages, making them unintelligible to their adversaries without the knowledge of the key. In the Caesar cipher, each letter in the plaintext is shifted by a fixed number of positions in the alphabet. Mathematically, this can be represented using modular arithmetic. Let's denote \( n \) as the shift value (the key) and \( P \) as the position of a letter in the alphabet. The Caesar cipher encryption function \( E \) can be expressed as: \[ E(P) = (P + n) \mod 26 \] Where \( \mod 26 \) ensures that the result wraps around the alphabet. For example, if \( n = 3 \) and \( P = 1 \) (representing 'A'), the encrypted letter would be \( E(1) = (1 + 3) \mod 26 = 4 \), which corresponds to 'D'.
52.How about shifting the alphabets by 1 letter each?What is the problem here?
Sol.
Shifting each letter of the alphabet by one position, known as a Caesar cipher with a fixed key of 1, is a simple form of substitution cipher. While it provides a basic level of encryption, it suffers from a significant vulnerability: its lack of security due to its limited key space. Since there are only 25 possible keys (each shift value from 1 to 25), an attacker can easily perform a brute-force attack by trying all possible keys to decrypt the message. This means that the encrypted message can be deciphered through only 25 trials, making it highly vulnerable to cryptanalysis.
53.Try encoding the word “VICHARANASHALA” using the above method (But shift 4 letters this time)
Sol.
To encode the word "VICHARANASHALA" using a Caesar cipher with a shift of 4 letters, we shift each letter in the word by four positions in the alphabet: - V becomes Z - I becomes M - C becomes G - H becomes L - A becomes E - R becomes V - A becomes E - N becomes R - A becomes E - S becomes W - H becomes L - A becomes E - L becomes P - A becomes E So, "VICHARANASHALA" would be encoded as "ZMGLEREVREWEP".
54.What if you have only the encoded message? How will you get to the original message?
Sol.
If we only have the encoded message and no knowledge of the key (the shift value used in the Caesar cipher), we would need to employ cryptanalysis techniques to decrypt the message. One common approach is frequency analysis, which relies on the fact that certain letters appear more frequently than others in natural language text. For example, in English, the most common letters are 'E', 'T', 'A', 'O', and 'I'. By analyzing the frequency of letters in the encoded message and comparing it to the expected frequency distribution of letters in English text, we can make educated guesses about the shift value. Another method involves trying all possible shift values (from 1 to 25) and examining the decrypted text for meaningful words or patterns. This brute-force approach would involve decoding the message 25 times with different shift values until the original message is revealed.
55.What if we substitute each letter by some other letter using a pre- defined mapping (eg.a->t,b->f,c->y,…)?How many trails do we have to do so that we can reach the secret message if we only have the encoded text and not the mapping ?
Sol.
If we have an encoded message using a substitution cipher with a predefined mapping, and we don't know the mapping, we essentially face a cryptanalysis problem. The number of possible mappings in a substitution cipher depends on the size of the alphabet used in the encoding. For example, if we're using the English alphabet, which consists of 26 letters, there are \( 26! \) possible permutations of the alphabet. Therefore, without knowing the mapping, we would need to try each possible permutation to decipher the message. This brute-force approach would require checking all \( 26! \) mappings, which is clearly impractical due to the vast number of trials involved. In summary, if we only have the encoded text and not the mapping used in a substitution cipher, it is practically infeasible to decipher the secret message by trying all possible mappings.
56.Is there any efficient approach for the second part of the 55th question?
Sol.
Yes, there are more efficient approaches for decrypting a message encoded with a substitution cipher when the mapping is unknown. One common technique is frequency analysis. In most languages, including English, certain letters occur more frequently than others. Here's how frequency analysis works: 1. Count the frequency of each letter in the encoded message. 2. Compare the frequency distribution to the expected frequency distribution of letters in the language being used (e.g., English). 3. Identify common patterns, such as single-letter words or repeated sequences, which may correspond to common letters or words in the language. 4. Use these patterns to make educated guesses about the mapping, such as which encoded letter corresponds to 'E' or 'T'. 5. Once a few letters are deciphered, use context and word patterns to further decrypt the message.
57.What do you think is the frequency of occurence of various letters in a sample English text? Which letter do you expect to be the most frequent ?
Sol.
In a typical English text, the frequency of occurrence of various letters follows a well-known distribution. The most frequent letter in English text is 'E', followed by 'T', 'A', 'O', 'I', 'N', 'S', 'H', 'R', 'D', 'L', 'C', 'U', 'M', 'W', 'F', 'G', 'Y', 'P', 'B', 'V', 'K', 'J', 'X', 'Q', and 'Z', in descending order of frequency. These frequencies can vary slightly depending on the specific text and context, but they provide a general guideline for the relative occurrence of letters in English text.
58.Assuming that an English text follows a particular order of frequency,can you solve the 56th question?
Sol.
Assuming that the English text follows the typical order of letter frequency, we can use this knowledge to help decrypt a message encoded with a substitution cipher. Given the encoded message, we can analyze the frequency of letters in the text. By identifying the most frequently occurring letter in the encoded message, we can make an educated guess that it corresponds to the most frequent letter in English text, which is 'E'. Once we determine the mapping for this letter, we can continue deciphering the rest of the message based on context and patterns. This process can be iterated, gradually revealing more letters and improving our understanding of the mapping until the entire message is decrypted. While frequency analysis provides a powerful tool for decrypting substitution ciphers, it may still require some manual effort and linguistic knowledge, especially for longer messages or messages with less predictable patterns. However, by leveraging the knowledge of letter frequency in English text, we can significantly reduce the number of trials needed to decrypt the message compared to a brute-force approach.
59.Suppose we take a subset from a huge text i.e \(k^{th}\), \(2k^{th}\), \(3k^{th}\)… elements.Will they also follow the same pattern observed in the previous question?
Sol.
Yes, if we take a subset of characters from a large enough English text, such as every \(k^{th}\) character, \(2k^{th}\) character, \(3k^{th}\) character, and so on, they are likely to follow a similar pattern of letter frequency as observed in the previous question. This is because the frequency distribution of letters in English text is relatively stable across different texts, assuming the text samples are large enough and representative of typical English language usage. Therefore, even when considering a subset of characters from a large text, we would still expect the most frequent letters to be 'E', 'T', 'A', 'O', 'I', and so on, in roughly the same order of frequency. Of course, the specific frequencies may vary slightly depending on the particular text and context, but the overall pattern of letter frequency should remain consistent. This consistency is what allows frequency analysis to be an effective technique for decrypting substitution ciphers, even when working with subsets of text.
60.Assume you arrange two meaningful english text strings in front of each other. What is the expected number of collisions in the letters? Call it “collision frequency”.
Sol.
To calculate the expected number of collisions in the letters of two meaningful English text strings arranged in front of each other, we follow these steps:1. Frequency Distribution: Define the frequency distribution of characters in English text. Denote the probability of occurrence of each character as \( p \), where \( i \) ranges from 1 to \( N \), the total number of characters in the English alphabet.
2. Collision Probability for Each Character: Calculate the collision probability for each character, denoted as \( P_{\text{collision}, i} \). This can be calculated as the square of the probability of occurrence of that character: \( p_i^2 \).
3. Collision Frequency: The expected number of collisions in a position is the sum of the collision probabilities for all characters. Denote the collision frequency as \( \text{collision frequency} \), which can be calculated as the sum of \( P_{\text{collision}, i} \) over all characters: \[ \text{collision frequency} = \sum_{i=1}^{N} p_i^2 \] Total Number of Collisions = N * Collision frequency.
61.Assume that in the previous question ,we apply the ceaser cypher(the one discussed in the first few questions), on both the strings, and alphabet by 5 letters then will the collision frequency remain the same?What if we shift first string by 3 letters and second by 5?
Sol.
Applying the Caesar cipher to both strings by shifting each letter by the same amount will not change the collision frequency. This is because the relative positions of the characters within each string remain the same, only their actual representations change.However, if we shift the first string by a different amount than the second string, it will affect the collision frequency. This is because the relative positions of characters within each string will change, leading to a different distribution of characters and hence a different collision frequency.
62.Suggest any such method using which we can be confident that the encoded text can’t be decoded by the enemy. (We may discuss it in further classes)
Sol.
Project 1- Vigenere Cipher
Module G
63.A dart is thrown at random onto a board that has the shape of a circle as shown below. Calculate the probability that the dart will hit the shaded region.
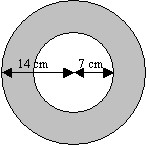
Sol.
The shaded region is the difference in area between two concentric circles (a larger circle and a smaller circle). - The radius of the larger circle \( R \) is 14 units. - The radius of the smaller circle \( r \) is 7 units. The area of the shaded region \( A_{\text{shaded}} \) is given by the difference in the areas of these two circles: \[ A_{\text{shaded}} = \pi R^2 - \pi r^2 \] Substituting the values: \[ A_{\text{shaded}} = \pi (14^2 - 7^2) \] \[ A_{\text{shaded}} = \pi (196 - 49) \] \[ A_{\text{shaded}} = \pi \cdot 147 \] The total area \( A_{\text{total}} \) is the area of the larger circle: \[ A_{\text{total}} = \pi R^2 \] Substituting the value: \[ A_{\text{total}} = \pi \cdot 14^2 \] \[ A_{\text{total}} = \pi \cdot 196 \] The probability \( P \) of a dart hitting the shaded region is the ratio of the area of the shaded region to the total area of the circle: \[ P = \frac{A_{\text{shaded}}}{A_{\text{total}}} \] Substituting the areas calculated: \[ P = \frac{\pi \cdot 147}{\pi \cdot 196} \] \[ P = \frac{147}{196} \] Simplifying the fraction: \[ P = \frac{147 \div 49}{196 \div 49} \] \[ P = \frac{3}{4} \] Thus, the probability of a dart hitting the shaded region is \( \frac{3}{4} \) or 0.75.64.Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
Sol.
To find the mean or expectation of the random variable X, which represents the sum of the numbers on two dice, you can use the formula: \[ \text{Mean} (\mu) = \sum_{i=2}^{12} i \times P(X=i) \] Where \( P(X=i) \) is the probability that the sum of the two dice equals \( i \). The sum can range from 2 (if both dice show 1) to 12 (if both dice show 6). The probability of getting each sum can be calculated by considering all possible combinations of the dice. Here's a table of the sums and their probabilities: \[ \begin{array}{|c|c|} \hline \text{Sum} & \text{Probability} \\ \hline 2 & \frac{1}{36} \\ 3 & \frac{2}{36} \\ 4 & \frac{3}{36} \\ 5 & \frac{4}{36} \\ 6 & \frac{5}{36} \\ 7 & \frac{6}{36} \\ 8 & \frac{5}{36} \\ 9 & \frac{4}{36} \\ 10 & \frac{3}{36} \\ 11 & \frac{2}{36} \\ 12 & \frac{1}{36} \\ \hline \end{array} \] Now, calculate the mean: \[ \mu = (2 \times \frac{1}{36}) + (3 \times \frac{2}{36}) + (4 \times \frac{3}{36}) + \ldots + (12 \times \frac{1}{36}) \] \[ \mu = \frac{2}{36} + \frac{6}{36} + \frac{12}{36} + \ldots + \frac{12}{36} \] \[ \mu = \frac{1}{36} \left(2 + 6 + 12 + \ldots + 12 \right) \] \[ \mu = \frac{1}{36} \times (252) \] \[ \mu = \frac{1}{36} \times 252 \] \[ \mu = \frac{252}{36} \] \[ \mu = 7 \] So, the mean or expectation of \( X \) is approximately \( 7 \).
65.A factory produces items, and each item is independently defective with probability
0.2. If 100 items are produced in a day, what is the expected number of defective items?
Sol.
To find the expected number of defective items produced in a day by the factory, we use the concept of expectation in probability theory. Given: - Each item is defective with probability \( p = 0.2 \). - The number of items produced in a day \( n = 100 \). The expected number of defective items \( E(X) \) can be calculated using the formula for the expectation of a binomial distribution: \[ E(X) = n \cdot p \] Substituting the given values: \[ E(X) = 100 \cdot 0.2 \] \[ E(X) = 20 \] Thus, the expected number of defective items produced in a day is 20.
66.A point is chosen at random inside a sphere of radius R. What is the probability that this point is closer to the center of the sphere than to its surface?
Sol.
To find the probability that a randomly chosen point inside a sphere is closer to the center than to its surface, we analyze the problem geometrically. Given: - The sphere has a radius \( R \). - We need to find the probability that a point is closer to the center than to the surface of the sphere. - A point inside the sphere is closer to the center than to the surface if its distance from the center is less than half the radius of the sphere, \( \frac{R}{2} \). The volume \( V_{\text{inner}} \) of the sphere with radius \( \frac{R}{2} \) is given by: \[ V_{\text{inner}} = \frac{4}{3} \pi \left( \frac{R}{2} \right)^3 = \frac{4}{3} \pi \cdot \frac{R^3}{8} = \frac{1}{6} \pi R^3 \] The volume \( V_{\text{total}} \) of the sphere with radius \( R \) is given by: \[ V_{\text{total}} = \frac{4}{3} \pi R^3 \] The probability \( P \) that a randomly chosen point inside the sphere is closer to the center than to the surface is the ratio of the volume of the inner sphere to the volume of the entire sphere: \[ P = \frac{V_{\text{inner}}}{V_{\text{total}}} = \frac{\frac{1}{6} \pi R^3}{\frac{4}{3} \pi R^3} = \frac{\frac{1}{6}}{\frac{4}{3}} = \frac{1}{6} \cdot \frac{3}{4} = \frac{1}{8} \] Thus, the probability that a randomly chosen point inside the sphere is closer to the center than to its surface is \( \frac{1}{8} \).
67.A point is randomly chosen inside a cube with side length 𝑎. What is the probability that the point is closer to one of the vertices than to the center of the cube?
Sol.
68.Imagine you have a number line that ranges from -1 to 1. You randomly pick k points on this line. What is the expected distance of the closest point to the midpoint of the line?
Sol.
Project 5- The Dart Game